Min mor har en spinderok på sit arbejdsværelse, hvis hjul har ni eger. Min papfar havde i noget tid funderet over nidelingen, da det ham bekendt ikke er muligt at tredele (og dermed heller ikke nidele) en vinkel uden en vinkelmåler. Den ydmyge snedker har i tidligere tider måske kun haft adgang til passer og lineal, og min papfar stillede mig derfor for sjov opgaven at finde ud af, hvordan en cirkel kan inddeles i ni lige store dele uden brug af en vinkelmåler – dvs. kun vha. passer og lineal.

Jeg er tilbøjelig til at give min papfar ret i, at opgaven næppe kan løses på de betingelser. Ikke desto mindre fandt jeg frem til en metode, som inddeler en cirkel i ni NÆSTEN lige store dele, og som i praktisk forstand sagtens kunne bruges. Så herunder er mit bud på, hvordan den ferme snedker (måske) har nidelt sin cirkel:

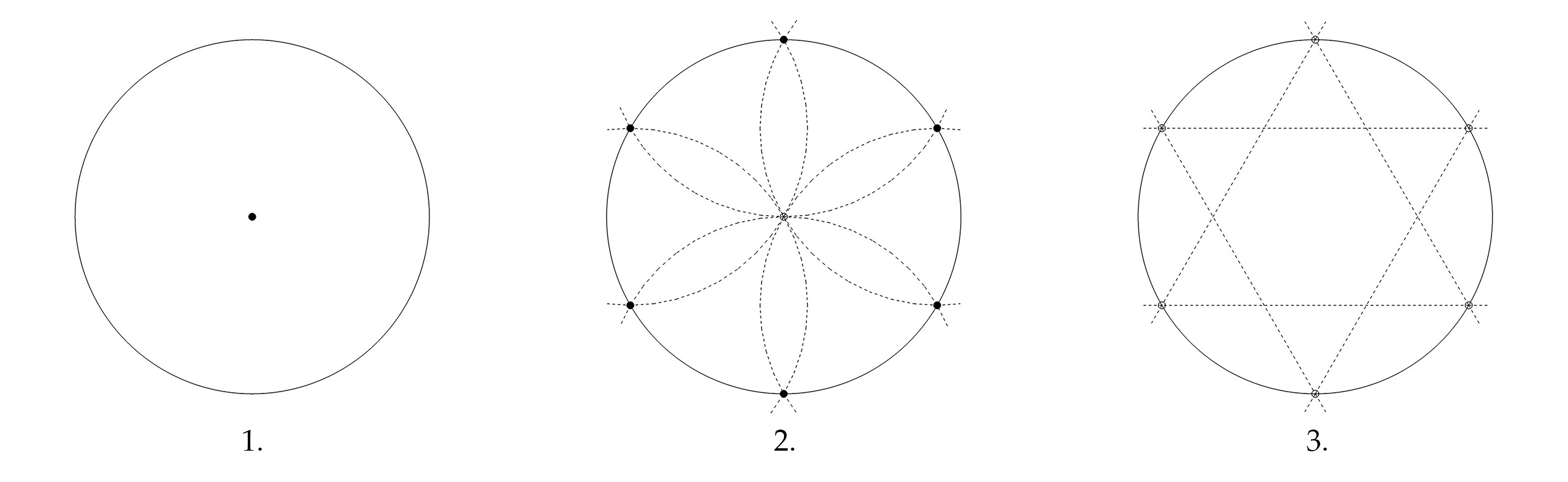
1. Han tegner sin cirkel.

2. Han tegner seks cirkelslag med samme radius som cirklen og med centrum i de øvrige cirkelslags skæringer med cirkelperiferien.

3. Han tegner linier mellem de seks skæringspunkter (sjettedelspunkterne), så der dannes to ligesidede trekanter.

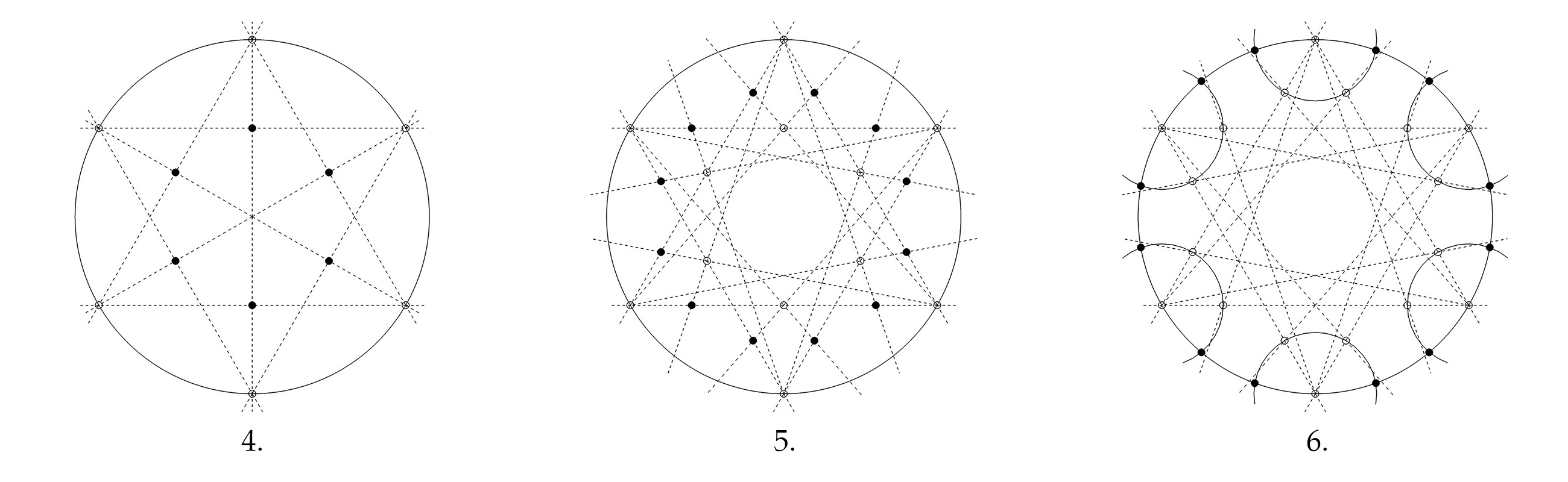
4. Han tegner linier mellem de modstående sjettedelspunkter, så der dannes skæringspunkter i midten af trekanternes sider.

5. Han tegner linier gående fra hvert sjettedelspunkt ud gennem midtpunkterne i trekanternes sider, så der længere ude dannes nye skæringspunkter med den anden trekants sider.

6. Han tegner seks cirkelslag med centrum i sjettedelspunkterne og med radius ud til skæringspunkterne fra forrige trin, så cirkelperiferien skæres i 12 yderligere punkter.

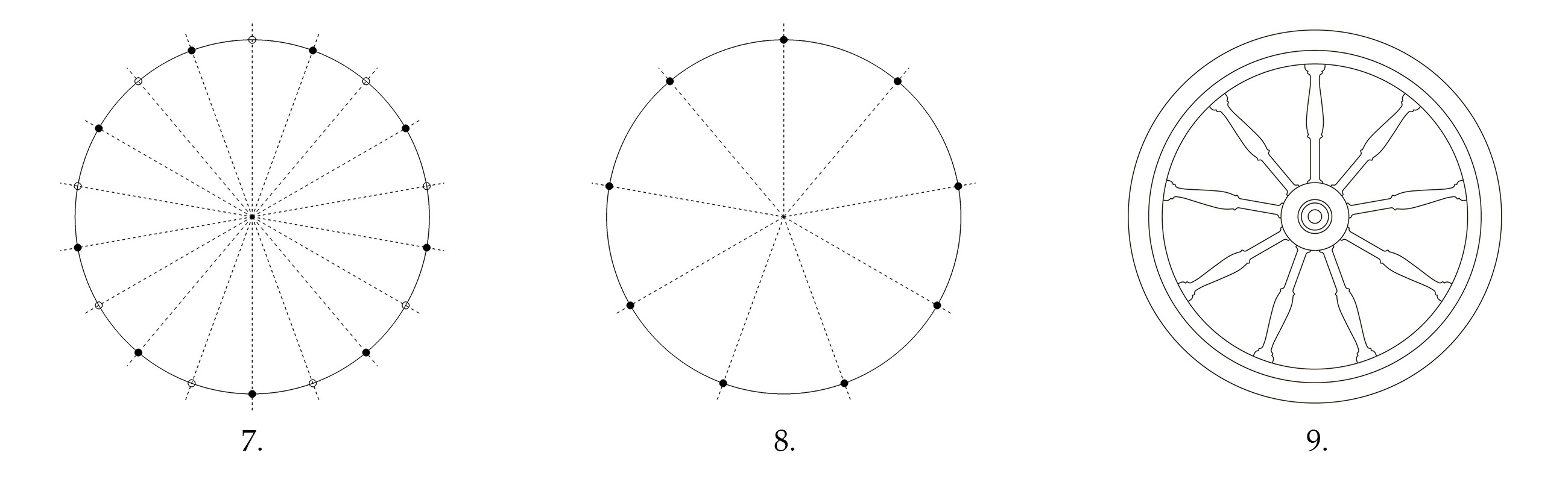
7. Han ser, at hans cirkel nu er inddelt med 18 punkter i 18 cirkeludsnit. Han fjerner hvert andet punkt.

8. Han ser, at hans cirkel nu er inddelt med ni punkter i ni cirkeludsnit, der hver ligger inden for 0,1° af 40° og i al praktisk forstand kan anses som værende lige store.

9. Han kan nu færdiggøre sit snedkerarbejde, f.eks. som hér et hjul til en spinderok inddelt med ni eger.

Et link til en printbar udgave af metoden (i PDF-formet, A4) kan findes under "DATA" for projektet.

Jeg har ikke fundet metoden ovenfor beskrevet andre steder. Til gengæld har jeg siden erfaret, at det kan lade sig gøre at inddele en cirkel i ni PRÆCIS lige store dele, hvis man, foruden passer og lineal, også må bruge en 90° snedkervinkel – et stykke værktøj, som den ydmyge snedker formentlig også har haft adgang til. Meeen det er jo lidt snyd ift. den stillede opgave ...